

Für diesen Stoß müssen einige geometrische Überlegungen gemacht werden. Dazu soll die folgende Skizze dienen.
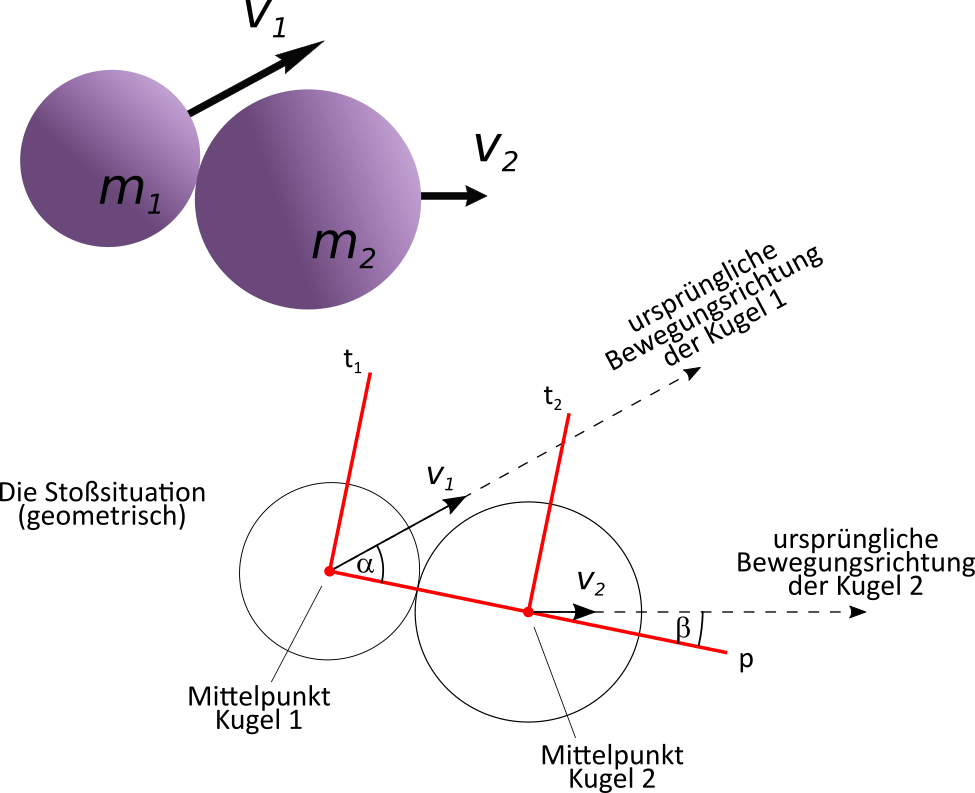
Der im untereren Teil dargestellte Zeitpunkt ist der, zu dem sich die Oberflächen der beiden Kugeln berühren. Die Geometrie ist dann so, dass die Verbindungslinie der beiden Mittelpunkte der Kugeln genau senkrecht durch die beiden sich berührenden Oberflächen verläuft. Das ist die rote Linie $p$. Die beiden Linien $t_1$ und $t_2$ wiederum sind senkrecht zu $p$, so dass sie tangential zu beiden Oberflächen an der Berührstelle zum Zeitpunkt des Stoßes verlaufen.
Die Geschwindigkeit $v_1$ wird nun in die Richtungen der Linien $p$ und $t_1$ aufgeteilt. Das gleiche passiert mit $v_2$ in die Richtungen der Linien $p$ und $t_2$. (➜ vgl. Schiefe Ebene)
Beide Geschwindigkeitsanteile in $p$-Richtung, also $v_{1,p}$ und $v_{2,p}$ werden wie beim elastischen Stoß behandelt, d.h. mit den beiden Formeln für die Geschwindigkeiten nach dem Stoß kann man $u_{1,p}$ und $u_{2,p}$ berechnen.
$$ u_{1,p} = \frac{\left( m_1 - m_2 \right) v_{1,p} + 2 m_2 v_{2,p}}{\left( m_1 + m_2 \right)} \\ \\ u_{2,p} = \frac{\left( m_2 - m_1 \right) v_{2,p} + 2 m_1 v_{1,p}}{\left( m_1 + m_2 \right)} $$Die beiden Anteile in $t$-Richtung werden durch den Stoß gar nicht verändert. Die Bewegungsrichtungen laufen an der Stoßstelle vorbei. Die Geschwindigkeiten nach dem Stoß sind somit $$ u_{1,t_1} = v_{1,t_1} \\ \\ u_{2,t_2} = v_{2,t_2} $$
Die Geschwindigkeit $u_1$ bzw. $u_2$ kann nun wieder zusammengesetzt werden:
Die Größe der Geschwindigkeit, d.h. der Betrag ist
$$
|u| = \sqrt{\left(u_{p}\right)^2 + \left( u_t \right)^2}
$$
Die Richtung bezüglich der $p$-Richtung ist
$$
\varphi = \arctan \left( \frac{u_t}{u_p} \right)
$$
Betrachtet werden sollte noch die Herkunft der beiden Winkel $\alpha$ und $\beta$. Dazu eine Skizze der Stoßsituation von oben:
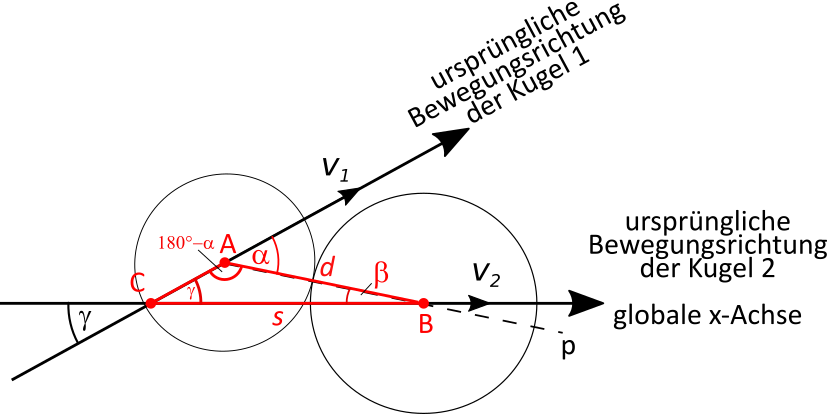
Zunächst eine Festlegung. Die Bewegungsrichtung der Bewegung von Kugel 2 dient als $x$-Achse, d.h., alle Winkel beziehen sich auf diese
Richtung. Ist die Geschwindigkeit der Kugel 2 vor dem Stoß gleich Null, wird die $x$-Achse (im Grunde beliebig) festgelegt.
Die Linie $p$ bezeichnet die Verbindungslinie der Kugelmittelpunkte beim Stoß. Der Abstand der Mittelpunkte ist $d = r_1 + r_2$ und ist konstant. Die Bewegungsrichtung der Kugel 1 schließt mit $p$ einen Winkel $\alpha$ ein, die Bewegungsrichtung der Kugel 2 und $p$ einen Winkel $\beta$. Weiterhin gilt, dass die beiden Bewegungsrichtungen der Kugeln einen Winkel $\gamma$ einschließen. Damit folgt: $\alpha = \beta + \gamma$.
Die für die Geometrie wichtigste Frage ist nun, in welchem Abstand $s$ befinden sich die Kugelmittelpunkte, wenn sich der Mittelpunkt der Kugel 1 auf der $x$-Achse befindet?
Ist neben dem Winkel zwischen den Bewegungsrichtungen $\gamma$ auch $s$ bekannt, kann mit Hilfe des Sinussatzes der Winkel $\alpha$ berechnet werden, denn es gilt: $$ \frac{\sin \alpha}{s} = \frac{\sin \gamma}{d} $$ Dabei wird ausgenutzt, dass $\sin \left( 180\text{°} - \alpha \right) = \sin \left( \alpha \right)$ ist.
Wenn allerdings die Lage der Linie $p$ bekannt ist, können die Winkel $\alpha$ und $\beta$ gleich bestimmt werden.
Um den elastischen Stoß in einer allgemeinen Form berechnen zu können, sind viele Parameter zu berücksichtigen. Wenn sich die beiden Stoßpartner entlang der Verbindungslinie der beiden Mittelpunkte $p$ bewegen, liegt der Grenzfall für den elastischen Stoß vor. Es gibt keine Aufteilung der Bewegung in zwei senkrecht zueinander stehenden Richtungen.
Der allgemeinere Fall liegt dann vor, wenn die Bewegungsrichtungen beider Stoßpartner beliebig sind und wenn auch die Lage beider Körper zum Stoßzeitpunkt beliebig ist. Dazu gibt es hier ein GeoGebra-Applet, in dem die geometrischen Verhältnisse, insbesondere die beiden Winkel $\alpha$ und $\beta$ dargestellt werden.
Zu beachten: Der Stoßzeitpunkt ist dann erreicht, wenn die Strecke $d = 8$ ist. Weiterhin kann man aus der Richtungsdarstellung erkennen, wohin der Bewegungspfeil zeigt. Beispielsweise bedeutet die Richtung $\left( 2 ; 1,5 \right)$, dass man vom Pfeilstartpunkt zwei Einheiten nach rechts und eineinhalb Einheiten nach oben geht um zur Pfeilspitze zu gelangen. Die Länge des Pfeils wäre dann $l = \sqrt{2^2 + 1,5^2} = 2,5$ Einheiten, der Winkel bezüglich der $x$-Achse wäre $\arctan{\left(\frac{1,5}{2}\right)} = 36,9$°.
Hinweis:
Die Lage des grünen Körpers kann verändert werden, indem man mit dem Mauszeiger auf den Rand zeigt und dann bei gedrückter
linker Taste die Maus bewegt.
Die Richtungen können verändert werden, indem man mit dem Mauszeiger auf den blauen Punkt mit dem Pfeil zeigt und bei gedrückter
linker Taste die Maus bewegt.
$d$ und die Winkel werden dann entsprechend angegeben.
© mondbrand MMXIX